Ergonautas - Lab      Publicaciones

ABSTRACT

Job rotation is a method of work organization by which working conditions can be improved. A change of activity reduces job monotony, fatigue, the risk of musculoskeletal disorders and cumulative trauma disorders. In order to develop a rotation plan that achieves the maximum benefit obtainable from this technique, the multiple factors that affect it must be considered simultaneously. This paper proposes a genetic algorithm that allows the planner to achieve job rotation schedules that aim to reduce the risk of musculoskeletal disorders, obtaining maximum diversification of the jobs carried out during working hours, and which take into account both permanent and temporary disabilities of the workers as well as their preferences. The fundamental contribution of the method lies in its focus on multi-criteria analysis and its ability to include new factors in the evaluation of solutions without the need to substantially modify the algorithm. This algorithm is then implemented by a computer program which thus becomes a flexible tool to aid the planner.

J.A. Diego-Mas^a*, S. Asensio-Cuesta^a, M.A. Sanchez-Romero^a, M.A. Artacho-Ramirez^a

^A Departamento de Proyectos de Ingeniería, Universidad Politécnica de Valencia, Edificio 5J, Camino de Vera s/n, 46020, Valencia, Spain.

*Corresponding author. E-mail address: jodiemas@dpi.upv.es (J.A. Diego-Mas)

Keywords: Job rotation scheduling; genetic algorithm; multi-criteria evaluation.

 Relevance to industry...

The results of this study suggest that the algorithm presented could be an efficient tool in the development of a rotation program, obtaining practical results within the scope of realistic possibilities of the plant.

Job rotation is a type of work organization whose use is becoming more widespread among manufacturing and service companies (Cosgel et al., 1999; Osterman, 1994). The benefits that can be obtained by setting up a job rotation system affect both the company and its workers. The costs associated with the introduction of such a system are low compared to other possible methods of improving working conditions (Kogi et al., 2003). From an organizational point of view, the rotation of workers means that operators are suitably trained to carry out different tasks, giving the company greater flexibility in assigning workers to different jobs, and thus reducing the impact of a high level of absenteeism. It also implies that the company becomes more familiar with the abilities of its workers, as long as their performance at different workstations can be monitored (Eriksson and Ortega, 2002; Ortega, 2001). On the other hand, setting up a job rotation system seems to have a positive influence on worker satisfaction (Triggs et al., 2000). Rotation implies a variation both in the content of the job to be performed, as well as in the skills and knowledge necessary for its execution. This results in the reduction of monotony and boredom, the decrease in absenteeism, an increase of the quality of the manufactured product, a reduction in stress, and a (long term) improvement in productivity (Miller et al., 1974). Furthermore, job variation reduces fatigue and the risk of suffering musculoskeletal disorders and cumulative trauma disorders (CTDs) (Grant et al., 1997; Hazard et al., 1992; Jonsson, 1988; Kuijer et al., 1999; Rissen et al., 2002), provided that the job changeovers involve an effective change in the muscle groups being utilized. Of course, rotation must not be considered as an alternative to redesigning those jobs that involve a risk factor. Rotation does not do away with risk, rather it “distributes” risk among various workers. Before including a job of this type in the rotation system, it must be correctly redesigned. Therefore, the correct workstation and tools design will decrease the amplitude of the risk, and the rotation program will decrease the frequency and the duration of the exposure (Winkel and Westgaard, 1996).

Besides the organizational difficulties involved in its introduction, the development of a rotation program is not an easy job due to the large number of criteria that must be considered for the correct assignation of workers to different jobs, as well as the large number of restrictions that must be imposed in order to obtain practical results within the scope of realistic possibilities of the plant. On the other hand, if the rotation program is not properly designed, it can have a negative effect on the working conditions (Putz-Anderson, 1988). This risk sharing approach can increase the global potential risk in the work group. Some studies show that using job rotation programs may not be as effective at reducing biomechanical injury risk factors as expected, and it can raise the risk of reporting low back pain due to the exposure to the peak loading parameters (Frazer et al., 2003). In Kuijer et al. (2005) was found that rotating groups of workers had more than two times higher risk of low back complains than non rotating groups. In Aptel et al. (2008) is shown that rotation has a positive impact on psychosocial factors and is relatively ineffective in relation to musculoskeletal disorders prevention. On the other hand, it is agreed that job rotation can provide psychosocial benefit. In Rissen et al. (2002), rotation is found to have a positive impact on the subjective perception about work done. Results of studies by St-Vincent et al. (2003) and Oullet et al. (2003) in car assembly lines showed that around 60% of workers considered that rotation reduced monotony and increased motivation in their work.

There is no definitive research about health benefits of job rotation as administrative solution but, in any case, if it is to be implemented, special care should be taken. It is therefore recommended that the job planner uses tools that enable him to create and evaluate rotations quickly and flexibly, taking into account all the aspects that impinge on correct job assignation and the restrictions that assure the viability of the results obtained. Although various approaches to the problem of job rotation have been studied (Carnahan et al., 2000, Tharmmaphornphilas et al., 2003), this paper sets about the subject by proposing a genetic algorithm which considers the conditions that maximize benefits from job rotation. In the process of generation of assignation alternatives the proposed algorithm considers that: the muscle groups involved in the various jobs performed by the worker in the different rotations should not be the same, the content of the jobs to be performed should involve an effective change of activity, and the preferences of the workers for certain jobs should be taken into account.

In this way, job monotony and the risk of suffering musculoskeletal disorders may be reduced. On the other hand, the ability of the workers to occupy a certain workstation depends on the state of their health. A slight musculoskeletal disorder, a reduction of visual or auditive capacity or a temporary or permanent physical or mental illness, could imply that a specific worker should not be assigned certain jobs which would require the use of impaired faculties, or which would involve harmful activities. Such is the case, for example, of workers with diabetes, epilepsy, slight osteopathy or myopia. This is of special importance due to the growing tendency to include handicapped workers among staff, an idea promoted by governments and institutions. The developed algorithm compares jobs requirements with worker abilities, so as to obtain a value describing the convenience of different worker allocations among the jobs. Also, the ability to consider restriction within the process of worker assignation provides the algorithm flexibility enabling the planner to veto assignations that, due to reasons of job organization, are not desired.

The problem under consideration belongs to the category of combinatorial optimization problems (Papadimitriou et al, 1982), specifically to the group of Timetabling and Scheduling problems, in which an attempt is made to locate the best configuration for a group of variables which, complying with certain restrictions, minimize (or maximize if necessary), a target function. The size of the solutions search space will depend on the number of rotations and on the number of jobs to be included in the rotation. In general, the search for acceptable solutions is a complex problem, especially when the number of imposed restrictions is high and when, as in the proposed case, the order in which jobs are assigned to the workers has an influence on the results obtained. The use of metaheuristics (Glover, 1986) in Timetabling Problems provides acceptable solutions without excessively prolonging the time of calculation. Within the Evolutionary Computation Algorithms, the Genetic Algorithms (GA) (Holland, 1975) are especially efficient at solving combinatorial optimization problems.

These algorithms perform a stochastic guided search based on the evolution of a set of structures, selecting the fittest ones in each cycle, as it occurs in natural species evolution. The starting point is a set of problem solutions called individuals. In the present work each individual is a job rotation schedule determining the worker position in each rotation. This first set is called initial population. Each individual is coded by a finite length chain (chromosome). The population undergoes several transformations that yield a new population (new generation). These transformations are guided by some genetic operators, being the most common “selection”, “crossover” and “mutation”, which combine or modify the chromosomes representing the individuals. For each generation, fitness of individuals in the population is calculated by means of a goal function. Using these values and some randomization, the fittest individuals are fostered to constitute the next generation. This process is repeated several cycles (generations) making the individuals evolve to better solutions to the problem. More information about GA can be found on (Chambers, 1995, 1998, 2000; Davis, 1991; Goldberg, 1989).

The developed GA (called DPI-ASEPEYO) was implemented in a software package with the objective of aiding the planner in the calculation of job rotation schedules. The software is designed to make this task flexible, and as systematic as possible. In this paper, the GA and the developed software are applied to obtain a job rotation schedule for a group of workstations within an automobile components supplier assembly plant. The paper is organized as follows; in Section 2 detailed information is given on the problem under consideration; in Section 3 the DPI-ASEPEYO algorithm and the software package developed for the solution of the problem are presented; Section 4 shows the results obtained, and in Section 5 conclusions are drawn and suggestions are given for future works.

The problem under consideration in this study was to obtain a job rotation schedule for a set of 18 workstations of an automobile parts supplier assembly plant. The 18 workstations all belonged to the same section and category and were the responsibility of one person. All were located in the same area and were sufficiently near to each other for the changeover at each rotation to cause no interruptions in the assembly process. The workers employed in the workstations had had sufficient training so as to be able to carry out the work involved in any of the workstations without the need for additional instruction. The working day was of eight hours, with a break of one hour for lunch at midday. The aim was to establish three rotations of two hours of duration, and a final rotation of one hour, making the start of the third rotation coincide with the end of the lunch break. With this temporary arrangement of the rotations, the aim was to distribute the changes in activity throughout the working day (AFS 1998).

2.1. Evaluation of workers and workstations

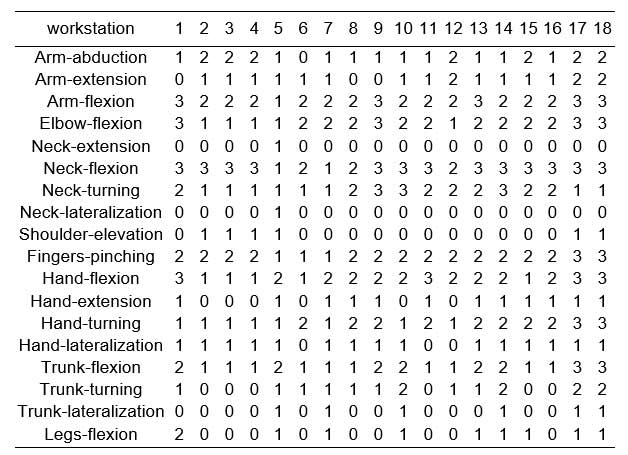
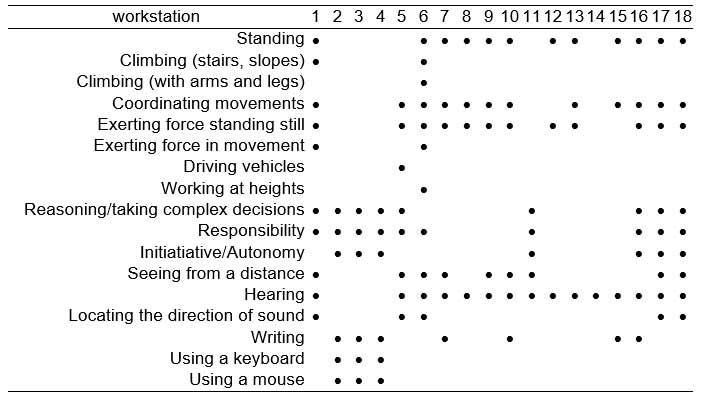
For the assignment of the workers to each of the 18 workstations, a total of 45 criteria were chosen (hereafter referred to as items) of four different types (Table 1).  The first group of items evaluates the movements an operative must carry out in performing the tasks of each workstation. These items were grouped according to the six principal muscle sets defined by Rodgers in his job evaluation technique (Rodgers, 1986; Rodgers, 1992), except for the group “Ankles/Feet/Toes”, which was not considered relevant for the tasks involved. The second group (General Abilities) included items that evaluate the general activities necessary for the different tasks. The third and fourth include certain mental and communicating abilities.

The 18 job workstations involved in the rotation were analyzed and assigned a score for each of the items considered in the “Movements” group. For this, the scoring system given in Table 2 was used. Scores were given between 0 and 3, increasing with the frequency of the movement throughout the course of the work undertaken at each workstation. Next, the abilities needed by the workers were determined for each of the workstations. Each of the items of the General, Mental and Communicating abilities groups was then classified as “Necessary” or “Not Necessary” according to whether the workstation required the ability indicated by the item. Lastly, the content of the activities of each workstation was analyzed and a group was formed of those in which the work performed was either exactly the same or did not involve an important change of the worker’s activities.

Subsequently, each worker’s ability to perform the movement indicated by each of the items in the Movements group was analyzed, using the scoring system given in Table 3, while the rest of the items were given a score of “Without limit” or “With Limit”, according to whether or not the worker was limited in the capability. The collaboration of the medical team of the plant was called upon in order to assign scores to workers with an illness or disability that limited their capability to undertake a certain activity or movement. Other workers were given a score of 0 or “Without limit” in all items. Finally, so as to take the workers’ preferences into consideration, they were asked to select those workstations they would rather not occupy from the 18 workstations in question.

Click Table to enlarge

Table 1:

Criteria used to assign workers to work workstations.

Click Table to enlarge

Table 2:

Score assigned to the movements required in a workstation according to frequency.

Click Table to enlarge

Table 3:

Score assigned to items according to worker’s capacity to perform the movement.

In this section we describe the GA developed for the assignation of workers to workstations according to ergonomic criteria, and the software developed to make its application the more flexible.

3.1.   The DPI-ASEPEYO genetic algorithm

The algorithm starts off by randomly generating a set of solutions (initial population) to the problem. Each solution (individual) is evaluated to determine its suitability for the requirements of the problem. Crossover and mutation operators are applied to the individuals of the initial population to create a new generation of individuals that inherit the best characteristics of their predecessors. For this purpose, the individuals that will participate in each of the genetic operators, and those that will survive and pass on to the following generation, are selected previously. The process is repeated with the new set of individuals until a certain number of iterations is reached, or until a certain number of iterations without a new best solution have been performed.

3.1.1. Generation of the initial population

The algorithm starts by generating an initial population of individuals that represent different solutions to the problem. Each individual is codified through a matrix of size n_wor x n_rot, n_wor being the number of participating workers (coinciding with the number of workstations in the rotation) and n_rot the number of rotations under consideration. A workstation is assigned at random to each cell of this matrix, taking care not to repeat the workstations within the same row. In the example given in Figure 1, worker nº 1 would occupy workstation nº 12 in the first rotation, nº 3 in the second, nº 7 in the third and nº 14 in the fourth. The number of individuals that make up the population (n_i) will depend on the characteristics of the problem, having obtained satisfactory results with a population of 50 individuals for the case of 18 workstations and 4 rotations. The population is codified through a vector of n_i individuals.

3.1.2. Evaluation of the individuals in the population

Each of the individuals that make up the population must be evaluated in order to determine the quality of the solution that it represents. An evaluating function resulting from the total of each of the criteria by means of a summation model (weighted sum) is employed. Each of the criteria considered in the evaluation is given a weighted coefficient which indicates its importance relative with regard to the other criteria. The solution is evaluated in two phases: in the first, the value of the items of each worker is modified according to the workstations occupied in previous rotations, so as to consider the cumulative effect of the different tasks carried out up to this point in time, and in the second phase the quality of the solution is calculated, using the value of the workers’ items obtained in the previous phase. Here, only the items corresponding to the Movements group are considered. The rest of the items will be considered later as penalizations.   

In the first phase, the initial value of each worker’s movement items is modified to obtain a different value for each rotation in a way that reflects the effects of the tasks carried out in previous rotations (the values of the workstations items will be constant for all the rotations). Thus, if a worker in a rotation occupies a workstation with a high value in a certain movement item, e.g. a frequent requirement for turning the neck, the analogous worker’s item, indicating his suitability for occupying the workstation, will be modified in order to reduce the probability of being assigned a workstation with similar requirements in future rotations. The degree of modification of the worker’s item will be larger the larger the duration of the task in question, and its effect will reduce according to the length of time that has passed since the task ended, gradually raising the probability of occupying a similar workstation.

Let us suppose that worker x is going to occupy a certain workstation in rotation r and that the workstations occupied by x in the rotations previous to r are known. Let w^x_j be the value of worker x items at the start of the working day (where j takes values between 1 and the number of items under consideration n_it), let a^x(k) be the workstation assigned to worker x in rotation k, and let p_j(a^x(k)) be the value of item j of the workstation assigned to worker x in rotation k. The process consists of calculating w^x_j(r) (the value of each of the j items of worker x in rotation r) as a function of the value of the items of previously occupied workstations. This calculation is carried out by means of a formula (equation (1)), which increases the original value of the worker’s item (w^x_j), as a function of the items corresponding to the workstations occupied in previous rotations if these items are over a certain threshold value (tre), the duration of each rotation and the time elapsed from the end of each rotation until the start of the current one. In equation (1) item j of worker x is calculated for rotation r. The greater the value of a worker’s item, the less is his suitability for performing activities of this type. The calculation formula implies that the longer the duration of the previous rotations and the shorter the time elapsed since they ended, the greater is their effect on the value of a worker’s item in the current rotation. If the value of the workstation item is not greater than the threshold value (tre), it does not affect the corresponding worker’s item. The tre parameter should indicate the value of the items below which it is considered not to cause any fatigue effects on the worker, and will not involve any risk of accumulative traumatic disorders if maintained through consecutive rotations. In the formula, t_k is the duration of the rotation k. d_k is the elapsed time since the end of rotation k until the start of the current one and includes the duration of the breaks between both rotations (p_k,r). f_red (reduction factor) is a parameter that defines the degree to which the algorithm considers that the task performed in a given rotation affects the value of the worker’s corresponding item in later rotations. During the studies, f_red was given a value of 3. Greater values determine a lower influence for previous job experience and vice-versa. This calculation will be performed for all the items of every worker involved in each of the rotations in order to obtain the values that are to be used in the second phase of the evaluation.

In the second phase of the evaluation, a value is obtained for the fitness (F) of each of the n_i individuals in the population. The level of suitability of the allocation of each worker to each of the tasks in the different rotations is evaluated. The suitability level is obtained by multiplying the value of the workers’ items by the corresponding workstation items to which they have been assigned in each rotation. Since the values of the workstation items are directly proportional to the necessity of performing certain activities in the course of the task, and those of the worker’s are inversely proportional to the suitability of the worker for the activities, the evaluating function (equation (2)) will give lower values for the individuals representing more suitable allocations. The evaluating function also considers the duration of each of the shifts (t_r), giving higher values to the shifts of longer duration. In this function n_wor is the number of workers, n_rot the number of rotations and n_it the number of items considered. C_j is a coefficient that indicates the relative importance of item j with respect to the rest of the items.

Each of the worker-workstations products is raised to the power of u (uniformity), which rewards solutions in which the workload is uniformly shared out among the workers. The objective is to avoid unbalanced assignations, where some workers are pushed to the limit while others are assigned less straining jobs in all the rotations. This means that the rise in F, due to overworked workers, is compensated by the slight increases caused by the workers with less-demanding jobs. The exponent u should be a positive value equal or greater than 1. Thus, the rise in F increases exponentially, due to the overloaded workers, penalizing the individuals that propose unbalanced solutions as opposed to those who provide more uniform solutions. Also, the assignation of handicapped workers, with a high value in a certain item, to workstations with a high requirement for this item, makes the worker-workstation product rise exponentially, penalizing the solutions who carry out such assignation.  

3.1.3. Application of penalizations

Rotation must involve a real change in the movements performed by the worker (Jonsson, 1988; Van Veltzer et al., 1992) as well as in the work content (MacLeod and Kennedy, 1993). These conditions are considered in the evaluation of the individuals. The probability of being assigned to a workstation with similar requirements in subsequent rotations is reduced, by causing a rise in the value of the movement items of the worker who has performed a given movement in a given rotation.

As was indicated in the section 2.1, the workstations were grouped according to work content during their evaluation. Given the form of the evaluation function (equation (2)), the allocation of a worker with low-value items to the same workstation in consecutive rotations would be valued positively. So, a penalty function is introduced to penalize the individuals that carry out these assignations. Thus, t_max is defined as the maximum time a worker can continuously spend in workstations of the same group. After the previously described evaluation process, the population is inspected analyzing the assignation realized by each individual. In the case of a worker occupying workstations in the same group in more than one consecutive rotation, the total time duration is calculated as the sum of the duration of each of these rotations. If the result is greater than t_max, this individual is penalized by increasing the value obtained by the evaluation function. His chances of survival in the succeeding generations are thus reduced.

The assignation of workers with limitations to perform a certain activity in a workstation where such an activity is required should also be penalized. An analysis is therefore made of the assignations carried out by the individuals of the population. The values of the items of the workstations in the groups General, Mental and Communication abilities are compared with those of the workers’ that occupy them. If a worker with a limitation in a certain item is found to occupy a workstation where this activity is necessary, the value obtained by the evaluation function is increased for this individual, thus reducing his chances of survival in future generations.

It may not be advisable to assign certain workers to certain workstations. This could be due to various reasons such as lack of ability to perform the task, or the worker’s personal preferences. Similar to the preceding case, individuals that carry out undesired assignations are penalized (increasing the value given by the evaluation function).

3.1.4. Selection

When all the individuals have been evaluated, a selection is made of those that will survive and pass on to the next generation or that will be used as reproducers. For this process a roulette wheel selection (Goldberg, 1989) is used, in which the probability of an individual being selected is inversely related to the value obtained in his evaluation, such that those individuals who offer the best assignations have greater chance of being selected. In the proposed algorithm, the best individual of a generation is always selected to go on to the next. This strategy (elitism) produced satisfactory results in the experiments carried out.

3.1.5. Reproduction

In the reproduction process, pairs of individuals are chosen from those selected in the previous stage. Reproduction is performed by means of a crossover, in which two new individuals are generated from the combination of the solutions represented by the original individuals. The new individuals will replace their parents in the population. The parameter p_c (crossover probability) determines the number of individuals in the next generation that will be created by crossover. A typical value for this parameter varies between 0.5 and 0.9 (Srinivas et al., 1994b). Figure 2 shows the reproduction process. The crossover point is chosen at random from a number between 1 and n_rot-1. The descendants are generated by combining the rotations that remain on the left and on the right of the crossover point in each of the parents. This method of performing the crossover guarantees that the descendents represent feasible solutions, since it prevents the same worker from being assigned to two different workstations in the same rotation.

3.1.6. Mutation

The mutation operator is applied to individuals selected at random. The number of individuals that will mutate is determined by the parameter p_m (probability of mutation). The process consists of selecting at random one rotation and two workers, and exchanging the jobs assigned to the workers in that rotation. For each individual this process is repeated as many times as is indicated by the parameter i_m (intensity of mutation). Thus, p_m defines the number of individuals that mutate, and i_m the magnitude of the variation of each individual. As in the case of the crossovers, the mutation operator is closed since it always produces individuals that represent feasible solutions. The individuals generated by mutation substitute their parents in the population. The value of p_m depends on the definition of the operator. A typical value for the parameter in the literature varies between 0 and 0.1, but it has been found in the experiments carried out in this work, that values between 0.2 and 0.4 provide good results (Srinivas et al., 1994b).

3.2 Software implementation

The GA developed aims to be an efficient tool to help the planner in the search for job rotation schedules that provide the maximum benefits obtainable from this technique. In the GA, many factors are taken into consideration to ensure that the results obtained are applicable to real situations without great modifications. This means that the amount of data to be introduced and the parameters to be defined for its processing are quite sizeable. To make the planner’s job easier, the algorithm was implemented in a software called MORE with the aim of obtaining the maximum flexibility in the introduction of data and processing parameters, the visualization of results and the utilization of the information generated (Figure 3). The software database enables data on workers and workstations to be stored and processed, as well as the parameters employed and the results obtained, which facilitates further calculation processes. The results are presented to the planner graphically, allowing him to make manual changes to the graphs, informing on the variation of the value of the evaluation function with regard to the original distribution. He is thus enabled to obtain distributions with changes as regards the original, so as to deal with situations in which, for whatever reason, it becomes necessary to change a worker’s job assignation without having to modify the complete job rotation schedule.

4 - Results

In this section the DPI-ASEPEYO method is used to obtain a job rotation schedule for the problem presented in Section 2, and the results obtained are exposed.

4.1. Evaluation of workers and workstations

After the evaluation it became clear that the item “trunk extension” had the same value in all the workstations and for all the workers, and it was therefore excluded from the calculation process. Also, within the items of the “Capacities” group, all those were eliminated in which all the workers were scored as “Without limit”. These items were: sitting, walking, using personal protection equipment, remaining in confined/restricted spaces, cooperating/working with others, attention/concentration, distinguishing colours, tactile sensitivity, smelling/tasting and speaking. It was decided not to include these items in the algorithm, because, since they all had the same value in all cases, they would introduce no variability in the calculation process. The evaluation of the workstations produced the results shown in Tables 4 and 5. The analysis of the type of activity carried out in each workstation enabled groups to be made of those with similar work content. Workstations 2, 3 and 4 were exactly alike in content and were therefore grouped together. Two other groups were also formed with very similar activities: workstations 9, 10 and 13 in one group and 17 and 18 in another.

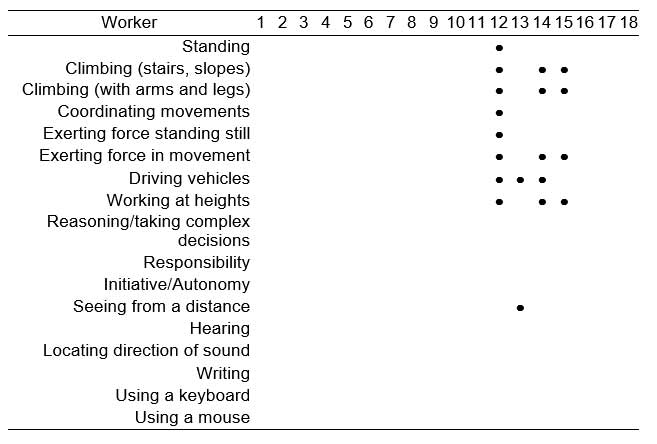
The results of the workers’ evaluation are given in Tables 6 and 7. Only workers 12, 14 and 15 had some type of problem that made certain movements difficult for them. In none of these cases did the plant’s medical staff consider that these difficulties prevented the worker from performing some kind of work if the movements in question were kept to a minimum. Table 7 shows the limitations of these workers in performing certain activities. Also, worker 13 had problems with long-distance vision that made it advisable for him not to drive vehicles. This worker had no trouble in performing any kind of movement. The workers’ preferences are shown in Table 8. The table shows the workstations the workers indicated they would rather not have to fill.

From these analyses the restrictions of the problem to be solved were determined by comparing the results obtained by the workers with those obtained by the workstations and the workers’ preferences. The penalized allocations are shown in Table 9. Finally, consecutive assignations to the workstations belonging to the same groups of activities, defined in Section 2.1, were penalized if the time limit allowed for working in similar workstations was exceeded. This limit will be defined in the following section.

4.2. Parameters employed and the job rotation schedule obtained

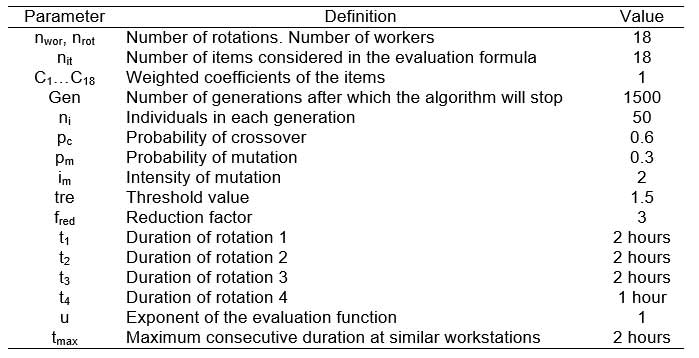
The different parameters of the algorithm have been described in previous sections. The values assigned to these parameters for solving the problem were based on experimental work previously carried out in which the most appropriate values were determined as a function of the number of workers and workstations in the rotation and the number of penalization. In these previous experiments, it had been observed that the algorithm is, in general, insensitive to small changes in the parameters. Table 10 gives the values chosen for each parameter for the solution of the problem under consideration. An adequate selection of tre and f_red parameters can considerably affect the obtained results. As a first approach, tre and f_redwere chosen following the plant’s medical and ergonomic staff advice. It will be needed to analyse the results of different job rotation schedules implementations obtained with different tre and f_red values in order to accurately set these parameters.

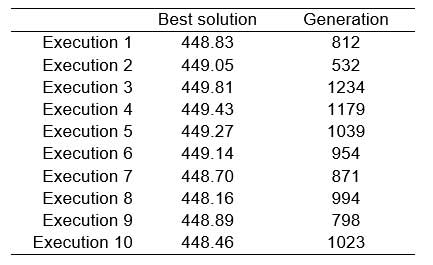
All the items employed in the calculation of the value of the target function were given the same importance, so that all the weighted coefficients took the value 1. The size of the population was fixed at 50 individuals and evolution was permitted up to generation number 1500. The algorithm was executed ten times in a PC equipped with a 1GHz processor and 256 Mb memory R.A.M., with an average execution time of 369.50 seconds. In the ten executions the algorithm evaluated 750,000 job rotation schedules. In Table 11 values are given for the fitness of the best individual found in each execution as well as for the generation in which he was found. The average value of these solutions is 448.97, the standard deviation is 0.48, and the value of the best individual is 448.16. In all cases the restrictions imposed on the problem are respected. Figure 4 gives the evolution of the value of the target function of the best individual during execution 8 and reflects the capacity of the algorithm to progressively generate better solutions by employing simulated evolution techniques. The graph shows a constantly decreasing evolution (except for very localized increases). This is due to the elitist strategy employed that prevents the algorithm from becoming disoriented. This advantage is counterbalanced by the danger of forcing the algorithm during the exploration to remain in specific zones of the search area where good solutions have been found in previous generations. One way of counteracting this is to employ high crossover and mutation probabilities to encourage the exploration of new zones. In the designed algorithm, the best individual of a generation is passed on to the next before applying the crossover and mutation operators, so that the elite individual may be subjected to variations that are reflected in localized peaks in the graph.

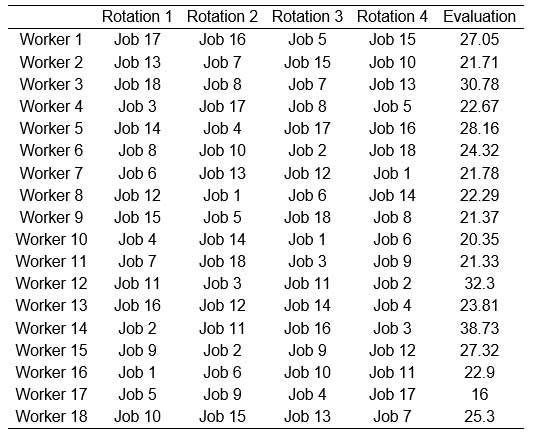
The best solution obtained is shown in Table 12. In this solution, the assignation of workers to workstations satisfy the restrictions imposed on the problem and reduce to a minimum the consecutive time consumed by the same movement. The workers are not assigned to similar workstations in two consecutive shifts, and, except in the case where a worker suffers some kind of handicap (workers 12 and 15), they do not occupy the same workstation again during the working day. In the last column of Table 12 the contribution of each worker to the target function is given, with the average value being 24.90, and the standard deviation 5.23. The high dispersion value indicates a certain imbalance among the workers in the assignation carried out. The most extreme case is the difference between worker 17, with a value of 16, and worker 14, with 38.73. This dispersion can be reduced by increasing the value of parameter u (exponent of the target function). When this parameter is increased, greater uniformity is obtained in the assignation of each worker, although this is counteracted by a rise in the total value of the target function. Thus, in ten experiments carried out, maintaining the previous parameters and increasing the value of u to 2, an average of 25.41 for the value of the assignation was obtained, with a dispersion of 4.07 and a mean value of the target function of 457.36.

As has been explained in Section 3.2.1, the initial value of the items of each worker is modified to obtain a different value for each rotation, such that it reflects the effect of the jobs carried out in previous rotations. The calculation formula implies that the value of a worker’s item in the current rotation is affected by the tasks carried out in previous rotations. The longer the duration of the rotation and the shorter the time elapsed since its completion, the greater the influence. Analyzing the evolution of the value of the workers’ items for each rotation in the case of the best solution obtained, it is possible to observe that, at the beginning of the second rotation the values are maintained or increased if the worker performed jobs during the first rotation which involved the movement corresponding to the item in question. It can be seen that, of the 324 cases (number of workers*number of items), in 117 there is an increase in the value of the workers’ items during Rotation 1. Rotation 2 thus begins with a greater value than the first, while in the rest of the cases it is constant. Out of these 117 cases, in 109 the algorithm has been able to assign workstations to the workers during Rotation 2 causing a decrease in the value of the items, i.e. workstations that do not involve intensive use of the movement indicated by the item. The remaining eight cases, in which a decrease in the value of the items did not occur, are distributed as follows: 4 correspond to “arm flexion”, 1 to “elbow flexion”, 1 to “finger pinching” and 2 to “hand flexion”. The movements related to these four items are performed in all the workstations with a high level of frequency, and it is therefore not possible to achieve a reduction. Also, between Rotations 2 and 3 there is a pause of one hour, which contributes to the decrease in the value of the items. Therefore, at the beginning of Rotation 3 the values of most of the items have fallen, so that the algorithm can, if the reduction is sufficient, once again assign to the workers workstations in which these movements are performed. It is also possible to observe that workers with limitations in any of the movements, and who thus have an initial value in the corresponding items other than 0, maintain this value throughout all the rotations. This means that they have not been assigned workstations that require intensive performance of these movements.

5 - Discussion

The development of a rotation program is not an easy job due to the large number of criteria that must be considered, as well as the large number of restrictions that must be imposed in order to obtain practical results. Although discussing a rotation schedule together with the involved workers is in fact a good practice, this is not enough to obtain all the benefits of this practice. More information and convenient tools are needed. If the number of involved workstations is high, the number of possible combinations is huge, and the best solution is to be searched among millions of feasible solutions. The program presented in this paper combines the information from workers (abilities, preferences…), and the requirements of the workstations to generate and evaluate solutions looking for the best combination. Planner must be careful when establishing a rotation schedule; if the rotation program is not properly designed, it can have a negative effect on the working conditions. In this sense, the proposed program helps the planner to decide considering all the factors involved in obtaining a good solution.

The application of genetic algorithms to solve the problem of generating job rotation schedules gives good results in less time than other methods such as integer programming (Carnahan et al., 2000). The DPI-ASEPEYO algorithm described in this paper approaches the problem with a multi-criteria focus, considering the different factors involved in obtaining solutions that maximize the benefits of job rotation systems. In evaluating the solutions, the algorithm considers not only the assignation of each worker in each shift, but also previous ones in previous rotations. In the example given, solutions were provided for the problem under consideration. The prolonged performance of movements of different parts of the body is minimized, the content of the tasks to be performed throughout the day is diversified, and the workers’ preferences are taken into consideration. The algorithm also account for the temporary or permanent disabilities of workers for certain jobs.

Any tool that assists in work organization must be flexible and applicable to the specific requirements of each production process and to the dynamics involved in such processes. As can be seen in Table 11, the algorithm presented in this paper is able to locate multiple job rotation schedules that adapt to the problem under consideration with small differences in values. The GA permits, given the addition model of the evaluating function, weighting each of the criteria considered, and gives the possibility of including new factors. Furthermore, the implementation of the algorithm in MORE application permits the management, exploitation, modification and re-utilization of information on workers, workstations and processes, as well as the storing of the job rotation schedules found and the production of reports on the latter. This makes it easier for the planner to find new solutions adaptable to changes in the production process, in the working hours, in job descriptions or in the abilities of the workers. If these changes do not modify the process greatly, it might be advisable to maintain the established job rotation schedule with a minimum of modification. Thus, if a worker were to be temporarily handicapped, MORE would allow a new job rotation schedule to be found, which with the minimum of changes to assignations, takes into account the change in the worker’s abilities.

The suggested procedure requires an initial effort for the evaluation of the workstations and workers involved in the rotations. Usually this information is available from previous studies carried out by ergonomic staff of the plant. If this information is accessible the calculation of different job rotation schedules is a simple task. It is a common practice to rotate workers in the same production line, where the tasks and procedures in each workstation are previously defined, and the rotation of the workers does not affect significantly the production plan. From our experience in the plants where the program has been implemented, this makes production planners to be well-disposed towards putting it into practice. The procedure shown in this work requires workers’ participation and opinions, thus facilitating job rotation implementation. Research by Oullet et al. (2003) shows that 21% of the workers were afraid of being moved to new positions due to rotation schedules, while 19% were worried about worse workmates relationships. Psychosocial issues may be crucial to make workers be predisposed to take part in a job rotation program. Its implementation should consider the participation and opinions of workers involved (Vézina, 2003).

Nevertheless, a deeper study of certain aspects of the tool is needed. Genetic algorithms are sensitive to execution parameters. For example, an inappropriate selection of the probabilities of mutation or crossover could cause a premature convergence of the algorithm to a local optimum or, on the other hand, an erratic search and the loss of orientation. A deeper study is needed on the sensitivity of the algorithm to the different parameters and on obtaining appropriate values for problems of different characteristics. The application by the planners in industrial plants of the algorithm proposed is providing feedback on the results obtained with different values for the parameters tre y f_red. The analysis of these results will allow determining the optimal values to maximize the benefits of rotation. However, obtaining these data is a long term process, as a long time is required to check the impact of job rotation on health and motivation of the workers. In a similar fashion, the coefficients that indicate the relative importance of each item with respect to the rest of the items must be object of a more detailed study. In the case of the problem presented in this work, as a first approach, all the coefficients have been assigned the same value, but the feedback obtained from the application of the algorithm will permit an assignation based on the influence of each item on the goodness of the results.

Going even further, it could be interesting to introduce self-adapting mechanisms for the different parameters as a function of the evolution of different generations (Srinivas et al., 1994a). Also, it would be advisable to consider other criteria for the assignation of workers to different workstations. The daily exposure of workers to noise during the different rotations should be kept to a minimum, which could be achieved by calculating the worker’s average level of exposure to noise in his job assignations (Tharmmaphornphilas et al., 2003). The lifting of weight or adopting static postures in each workstation could be evaluated by means of the Job Severity Index (Liles, 1986; Carnahan et al., 2000), the NIOSH lifting equation (Waters et al., 1993; Waters et al., 2007), the Rapid Entire Body Assessment (REBA) (Hignett et al., 2000), or the Rapid Upper Limb Assessment (McAtamney et al., 1993). The results of the application of each of these evaluating tools to the workstations could be included as items to be considered and included in the evaluating function with their corresponding weighted coefficients.

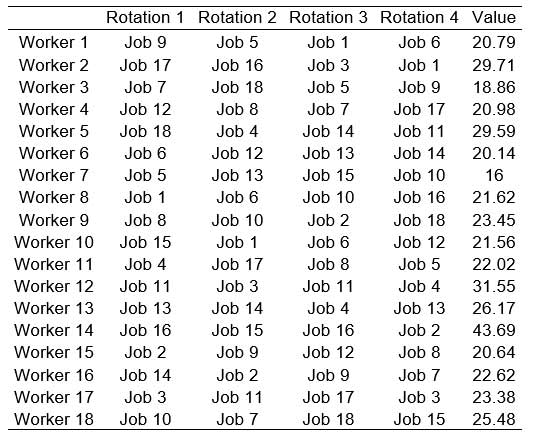
The duration and number of rotations and the pauses are established by the planner, based on the requirements of production and working hours of the plant. However, it would be interesting if the GA could help the planner in this task. In the problem considered in this study, a job rotation schedule of four rotations with a one-hour break between Rotations 2 and 3 was used. The rotations lasted two hours, except Rotation 4, which lasted one hour. For these conditions a solution was found with a value of 448.16 for the evaluating function and a mean value of 24.90 for the workload of each worker. An experiment was carried out reducing the break between Rotations 2 and 3 to 50 minutes and including a break of 10 minutes between Rotations 1 and 2. With these new conditions, and maintaining the other parameters of the problem, a new solution was obtained (Table 13) with a value of 438.26 for the target function and a mean value of 24.50 for the workload of each worker. The introduction of a new short break between rotations, in spite of reducing the duration of the already existing break, produced a significant improvement in the result. The search for the distribution and duration of suitable rotations and breaks can be performed by the algorithm, adding them to the codification of each individual. (Tharmmaphornphilas et al., 2004) have already dealt with this subject, although quantitively. In each individual’s codification, besides the worker that occupies each workstationin each rotation, the duration of the rotation and the distribution of breaks would be established (keeping total work and break times constant). This would mean that the mutation and crossover operators would have to be modified to account for the new codification, and limits would have to be establishment to prevent proliferation of what would be infeasible solutions in practice; for example, establishing the maximum and minimum number of breaks and the maximum and minimum durations of rotations and breaks.

Future research in this area must focus on the development of the algorithm, to expand its capacity for generating solutions to the problem of job rotation that account for the many factors involved. In this paper, we have suggested some lines of investigation that should be followed. Moreover, the use of MORE application by the planners in industrial plants will provide feedback on its use which will make this tool more flexible and adequate to particular cases.

• AFS, 1998, Ergonomics for the prevention of musculoskeletal disorders. Swedish National Board of Occupational Safety of Health, Solna, Sweden.
• Aptel, F., Cail, A., and Gerling, O. L., 2008, Proposal of parameters to implement a workstation rotation system to protect against MSDs. International Journal of Industrial Ergonomics, doi:10.1016/j.ergon.2008.02.006
• Blum, C. and Roli, A., 2003, Metaheuristics in combinatorial optimization: overview and conceptual comparison. ACM Computing Surveys, 35, pp. 268-308.
• Carnahan, B. J., Redfern, M. S. and Norman, B., 2000, Designing safe job rotation schedules using optimization and heuristic search. Ergonomics, 43, pp. 543-560.
• Chambers, L. D., 1995, Practical Handbook of Genetic Algorithms: New frontiers. 1st ed. Boca Raton: CRC Press, Inc.
• Chambers, L. D., 1998, Practical Handbook of Genetic Algorithms: Complex coding system. 1st ed. Boca Raton: CRC Press, Inc.
• Chambers, L. D., 2000, Practical Handbook of Genetic Algorithms: Applications. 2nd ed. Boca Raton: CRC Press, Inc.
• Cosgel, M. M. and Miceli, T. J., 1999, Job rotation: cost, benefits and stylized facts. Journal of Institutional and Theoretical Economics, 155, pp. 301-320.
• Davis, L., 1991, Handbook of Genetic Algorithms. New York: Van Nostrand Reinhold.
• Eriksson, T. and Ortega, J., 2002, The adoption of job rotation: testing the theories. French Economic Association Conference, Lyon.
• Frazer, M.B., Norman, R. W., Welles, R. P. and Neumann W. P., 2003, The effects of job rotation on the risk of reporting low back pain. Ergonomics, 46, pp 904-919.
• Glover, F., 1986, Future paths for integer programming and links to artificial intelligence. Computers & Operations Research, 13, pp. 533-549.
• Goldberg, D.E., 1989, Genetic Algorithms in search, optimization and machine learning. Massachusetts: Addison-Wesley Publishing Company Inc.
• Grant, K. A., Habes, D. J. and Bertsche, P. K., 1997, Lifting hazards at a cabinet manufacturing company: evaluation and recommended controls. Applied Occupational and Environmental Hygiene, 12, pp. 253-258.
• Hazard, L., Mautz, J. and Wrightsman, D., 1992, Job rotation cuts cumulative trauma cases. Personnel Journal, 71, pp. 29-32.
• Hignett, S. and McAtamney, L., 2000, Rapid Entire Body Assessment (REBA). Applied Ergonomics, 31, pp. 201-205.
• Holland, J.H., 1975, Adaptation in natural and artificial systems (University of Michigan Press: Ann Arbor).
• Jonsson, B., 1988, Electromyographic studies of job rotation. Scandinavian Journal of Work, Environment and Health, 14 , pp. 108-109.
• Kogi, K., Kawakami, T., Itani, T. and Batino, J. M., 2003, Low- cost work improvements that can reduce the risk of musculoskeletal disorders. International Journal of Industrial Ergonomics, 31, pp. 179-184.
• Kuijer, P.P.F.M., Visser, B. and Kemper, H.C.G., 1999, Job rotation as a factor in reducing physical workload at a refuse collecting department. Ergonomics, 42, pp. 1167-1178.
• Kuijer, P.P.F.M., Beek, A.J., Dieën, J.H., Visser, B. and Frings-Dresen, M.H.W., 2005, Effect of job rotation on need for recovery, musculoskeletal complaints, and sick leave due to musculoskeletal complaints: a prospective study among refuse collectors. American Journal of Industrial Medicine, 47, pp. 394-402.
• Liles, D. H., 1986, The application of the job severity index to job design for the control of manual materials handling injury. Ergonomics, 29, pp. 65-76.
• MacLeod, D. and Kennedy, E., 1993, Job rotation system. Report to XYZ CO, 12pp.
• McAtamney, L. and Corlett, E. N., 1993, RULA: A survey method for the investigation of work-related upper limb disorders. Applied Ergonomics, 24, pp. 91-99.
• Miller, F. G., Dhaliwal, T. S. and Mogas, L. J., 1973, Job rotation raises productivity. Industrial Engineering, 5, pp. 24-29.
• Ortega, J., 2001, Job Rotation as a Learning Mechanism. Management Science, 47, pp. 1361-1370.
• Osterman, P., 1994, How common is workplace transformation and who adopts it? Industrial Labour Relations Review, 47, pp. 173-188.
• Ouellet, S., Vézina, N., Chartrand, J., Perrier, P.P. and Malo, J.L., 2003, L’implantation de la rotation de postes: un exemple de démarche préalable. Pistes, 5, 24pp. .
• Papadimitriou, C. H. and Steiglitz, K., 1982, Combinatorial optimization: algorithms and complexity. (Dover Publications Inc: New York).
• Putz-Anderson, V., 1988, Cumulative trauma disorders: a manual for musculoskeletal diseases of the upper limbs. (Taylor & Francis Inc.: London).
• Rissen, D., Melin, B., Sandsjö, L., Dohns, I. and Lundberg, U., 2002, Psychophysiological stress reactions, trapezius muscle activity, and neck and shoulder pain among female cashiers before and after introduction of job rotation. Work & Stress, 16, pp. 127-137.
• Rodgers, S. H.,1986, Ergonomic design for people at work. Vol.II. Eastman Kodak Co.,
• Rodgers, S. H., 1992, A functional job analysis technique. Occupational medicine: State of the art reviews, 7, pp. 679-711.
• Srinivas, M. and Patnaik, L.M., 1994a, Adaptative probabilities of crossover and mutation in genetic algorithms. IEEE Transactions on systems, man and cybernetics, 24, pp. 656-667.
• Srinivas, M. and Patnaik, L.M., 1994b, Genetic algorithms: a survey. Computer, 27, pp. 17-26.
• St-Vincent, M., Vézina, N., Dufour, B., St-Jacques, Y. and Cloutier, E., 2003, La rotation des postes : ce qu'en pensent des travailleurs d'une usine d'assemblage automobile. Pistes, 5, 21pp., .
• Tharmmaphornphilas, W., Green, B., Carnahan, B. J. and Norman, B. A., 2003, Applying Mathematical Modeling to create Job Rotation Schedules for Minimizing Occupational Noise Exposure. American Industrial Hygiene Association Journal, 64, pp. 401-405.
• Tharmmaphornphilas, W. and Norman, B., 2004, A quantitative method for determining proper job rotation intervals. Annals of operations research, 128, pp. 251-266.
• Triggs, D.D. and King, P. M., 2000, Job rotation: an administrative strategy for hazard control. Professional Safety, 45, pp. 32-34.
• Van Velzer, C.T., 1992, Economic ergonomic interventions: the benefits of job rotation. Proceedings of the 25th Annual Conference of the Human Factors Association of Canada, October 25-28, pp.207-212.
• Vézina, N., 2003, Implantation de la rotation : quels sont les enjeux? Quelles sont les balises?. Pistes, 5, 20pp., .
• Waters, T. R., Putz-Anderson, V., Garg, A. and Fine, L. J., 1993, Revised NIOSH equation for the design and evaluation of manual lifting tasks. Ergonomics, 7, pp. 749-776.
• Waters, T. R., Lu, M.L., and Occhipinti, E., 2007, New procedure for assessing sequential manual lifting jobs using the revised NIOSH lifting equation. Ergonomics, 50, pp. 1761-1770.
• Winkel, J. and Westgaard, R.H., 1996, A model for solving work related musculoskeletal problems in a profitable way. Applied Ergonomics, 27, pp 71-7.

• J.A. Diego-Mas; S. Asensio-Cuesta, M.A. Sánchez-Romero; M.Á. Artacho-Ramírez 2009. A multi-criteria genetic algorithm for the generation of job rotation schedules. International Journal of Industrial Ergonomics, 39 (1), pp. 23–33.