The most common origin of musculoskeletal injuries due to physical load is the overload of joints, tendons, ligaments, and, in general, the body structures of the locomotor system. These overloads can result from excessive levels of effort, duration, and repetitiveness. In addition to injuries, muscle overexertion can cause discomfort and fatigue.
Determining whether an effort can be harmful is a complex task since it depends on multiple factors. On one hand, there are physiological factors such as the posture in which the effort is made, the muscle groups involved, or the speed at which the movement is performed. For example, each muscle has a different function and spatial arrangement that influences its ability to exert force depending on the adopted posture. The maximum contraction force of a muscle is approximately 8.5 kg per square centimeter of cross-section. However, this is only true if the muscle works at a normal level of contraction. When the muscle approaches its limits of contraction or stretching, its ability to produce force decreases, and if the effort involves movement, the level of contraction can vary during it. It is also known that the force developed by a muscle decreases with the speed at which the movement is performed.
On the other hand, there are individual and population factors. For example, the biomechanical capacity of men is 20% higher than that of women, and even among people with the same constitution, biomechanical capacity can vary considerably.
To accurately determine whether a particular action requiring the exertion of force can cause discomfort, fatigue, or injuries, it is necessary to consider all the mentioned conditioning factors. This is a complex task that, to some extent, can be addressed through biomechanical calculations (on Ergoniza you can find the software BIO-Mech for conducting biomechanical analyses). However, although biomechanical assessment allows for a detailed and specific risk evaluation, it can be costly to perform. The risk assessment method defined in the EN1005-3 standard (Recommended force limits for machine use) provides a simpler way to identify and quantitatively and qualitatively assess these risks.
Despite the greater simplicity of the method proposed in the EN1005-3 standard compared to other risk analysis techniques for exerted forces, the calculation process can be costly and requires certain mathematical and statistical knowledge. Therefore, it is recommended to use calculation software such as Forces - EN1005-3 that Ergoniza makes available to you.
Remember...
The most common origin of musculoskeletal injuries due to physical load is the overload of the body structures of the locomotor system. These overloads can result from excessive levels of effort, duration, and repetitiveness.
Remember...
The risk of overexertion depends on physiological, individual, and population factors.
The EN1005-3 Standard establishes the recommended force application limits and the calculation procedure for the associated risk levels, allowing the identification of potentially harmful situations or the proper design of machines and workstations. The standard is based on scientific evidence regarding physiology and epidemiology of manual work to establish the recommended force limits. For the calculation procedures, it sets certain statistical simplifications (based on the European population) that, although reducing the accuracy of the calculations, increase their applicability in practice in both the workplace and domestic settings. Thus, the standard is applicable to both workers (adults, healthy and with normal physical capacities) and the general population (including young people and the elderly).
The EN1005-3 Standard evaluates risk based on the force-generating capacity of users or workers following the general calculation scheme shown in Figure 2 (you can enlarge the image by clicking on it). Although the detailed calculation procedure will be explained later, a general description is provided now. As initial assumptions, it is considered that efforts can be made in an optimal way and under ideal circumstances, meaning with the appropriate position of the limbs and trunk, a range of motion within the permissible limits, proper force application direction, and allowing variation in movements and efforts performed. The calculation must be performed for each force application action present in the evaluated activity. Only if an action is infrequent or requires very little force can it be evaluated in a more general way.
There are three steps in the general calculation scheme:
In this first step, the type of force application action being evaluated and the potential user/worker population are considered. From this data, the statistical distribution of Isometric Forces for the evaluated action is established, and the Maximum Isometric Force (FB) for the potential user population is determined.
An isometric force is one in which, during its application, there is no variation in muscle length, and no movement of the load or the point of application of the resistant force occurs. The Maximum Isometric Force (FB) is obtained from the statistical distribution of Isometric Forces for the evaluated action, considering the maximum force a certain percentage of the population could exert without causing fatigue. The standard sets this protected population percentage at 85% when the calculation is performed for workers or professional users, and 99% when studying the general population.
To calculate the Maximum Isometric Force (FB), three different procedures can be used, which will be explained later, and are distinguished by their accuracy and calculation complexity.
Having determined the Maximum Isometric Force (FB) in the previous step, Step B considers the conditions under which the action is performed. As mentioned earlier, the risk depends not only on the magnitude of the force exerted but also on its duration, frequency, and speed. Based on these three factors, and the Maximum Isometric Force (FB), this step calculates the Reduced Maximum Isometric Force (FBr), also known as Corrected Isometric Force. This is the force that could be exerted without significant fatigue under the given conditions (type of action, worker/user population, speed, frequency, and duration of the action). To obtain FBr, multiply FB by a set of multipliers.
The standard establishes three risk zones for force application actions: Recommended, Not Recommended, and To be Avoided. Knowing the Reduced Maximum Isometric Force (FBr), the calculation proceeds by determining the Maximum Recommended Force for the evaluated action. This value is obtained by multiplying the value of FBr by a multiplier that depends on the desired risk zone for the action (generally, Recommended). Finally, by comparing the Maximum Recommended Force with the actual observed force, a Risk Index is obtained.
Remember...
EN1005-3 standard establishes the recommended force limits and the calculation procedure for the associated risk levels.
As initial assumptions, it is considered that efforts can be made in an optimal manner and under ideal circumstances.
The calculation must be performed for each of the force application actions present in the evaluated activity.
Remember...
In the general calculation scheme of EN1005-3 standard, three steps can be distinguished.
In STEP A, the Maximum Isometric Force (FB) for the potential user population is determined.
In STEP B, the Reduced Maximum Isometric Force (FBr) is determined, considering the duration, frequency, and speed of the action.
In STEP C, the risk level of the action is established from three possible levels: Recommended, Not Recommended, and To be Avoided
First, the worker's/user's activity will be analyzed in detail for tasks that require force application actions. Depending on whether an existing activity is being evaluated or a new activity is being designed, the actions will be either observed or anticipated to be performed. After the analysis, it will be established which actions will be evaluated. In general, the calculation must be performed for each observed action. Only if an action is infrequent or requires very little force can it be evaluated more generally.
Once the force application actions to be included in the evaluation are known, it will be established to which type of action each of them corresponds. The standard defines 13 possible action typologies divided into 4 groups shown below.

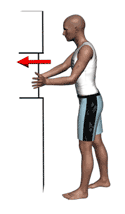
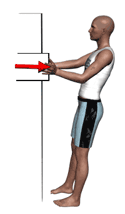

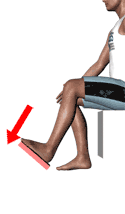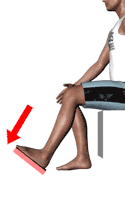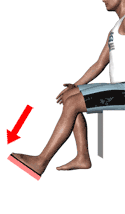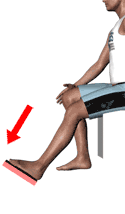






Since maximum isometric forces depend on gender and age, it must be established which workers/users will perform the actions. Different scenarios may arise:
The Maximum Isometric Force (FB) is obtained from the statistical distribution of Isometric Forces for the evaluated action, considering what maximum force a certain percentage of the population could exert without causing fatigue. The standard establishes that the percentage of the population that must be protected is 85% when calculating for professional workers or users, and 99% when studying the general population or in a domestic setting.
Once the force application actions to be evaluated, their types, the potential workers/users, their age and gender distribution, and the study's scope (professional or domestic) are known, it is possible to calculate the Maximum Isometric Force (FB). The standard provides three possible alternatives for calculating with different accuracy and complexity levels. Each of them can be used under certain conditions and assumes certain simplifications in the calculation, except for Alternative 3, which performs a more accurate calculation. The three calculation alternatives will be explained later in this document.
Age Women Men Under 20 years 1.6% 2.0% Between 20 and 50 years 31.6% 43.8% Over 50 years 7.6% 13.4% Table 1:
Percentage distribution of gender and age in the adult European workforce.
Remember...
In the Step A of the calculation procedure, you should:
Determine the force actions to evaluate. In general, the calculation should be performed for each of the observed actions.
Determine the type of actions. The standard defines 13 possible action typologies.
Determine potential workers/users. The options are: A single specific worker/user, multiple workers/users, or an estimated population.
Determine the protection level of the population. 85% should be protected when calculating for professional workers or users, and 99% when studying the general population or in a domestic setting.
Calculate the Maximum Isometric Force (FB). To do this, one of the 3 calculation procedures established by the standard will be used.
In Step A, the Maximum Isometric Force (FB) has been calculated. In Step B, the conditions under which the action is performed will be considered. As previously mentioned, the risk depends not only on the magnitude of the force exerted but also on its duration, frequency, and speed. Based on these three factors, and the Maximum Isometric Force (FB), the Reduced Maximum Isometric Force or Corrected (FBr) is calculated in this step. This is the force that could be exerted without significant fatigue under the given conditions (type of action, worker/user population, speed, frequency, and duration of the action).
To obtain FBr, multiply FB by three multipliers: speed multiplier (mv), frequency multiplier (mf), and duration multiplier (md).
FBr = FB * mv * mf * md
The force of contraction developed by a muscle decreases with the speed at which the movement is performed. The movement multiplier factor takes this fact into account by reducing the Maximum Isometric Force if the movement is fast. The value of mv is obtained from Table 2.
Repeatedly performing an action causes fatigue, which reduces the muscle's capacity to generate force. The degree of muscle contraction capacity reduction depends on both the duration and frequency of the action. Higher frequency and duration of the action result in a greater decrease in Maximum Isometric Force (FB). The value of mv is obtained from Table 3.
Fatigue produced by performing an action is cumulative, meaning it increases with the time the action is performed. Therefore, given a specific action, fatigue accumulates over time in the muscle groups involved in applying force depending on its duration. Additionally, other actions, though not identical to the one being evaluated, are similar because they activate the same muscle groups and also accumulate fatigue in them. To determine the duration multiplier factor (md), the duration of the action takes into account the working hours dedicated to the action being considered and those dedicated to all similar actions.
In conclusion, the total duration of the actions is the duration of the task in which the force actions are performed. It should consider the working time of the current action, including interruptions, as well as that of all similar actions. Similar actions are those performed in a similar posture with the same body part. For example, if the current action is pushing with one arm while seated, and there is another action pulling with one arm while seated, both would be similar actions, and when introducing the total duration of the actions, the combined duration of both should be considered. The value of mv is obtained from Table 4.
Movement speed mv Immobility or very slow movement 1 Noticeable movement 0.8 Table 2:
Speed multiplier (mv)
Action duration
(min)Action frequency
(min-1)≤ 0.05 > 0.05 ≤ 0.2 1.0 0.6 > 0.2 - 2 0.8 0.4 > 2 - 20 0.5 0.2 > 20 0.3 not applicable Table 3:
Frequency multiplier (mf)
Duration (h) ≤ 1 > 1 - 2 > 2 - 8 md 1.0 0.8 0.5 Table 4:
Duration multiplier (md)
Remember...
In Step B of the calculation procedure, the Reduced or Corrected Maximum Isometric Force (FBr) is calculated. This is the force that could be exerted without significant fatigue.
To calculate FBr, it is necessary to first compute: the velocity multiplier (mv), the frequency multiplier (mf), and the duration multiplier (md).
With the multipliers known, FBr is calculated using the formula: FBr = FB * mv * mf * md
In Step B, the Reduced or Corrected Maximum Isometric Force (FBr) has been calculated. This is the force that, under the given conditions (type of action, population of workers/users, speed, frequency, and duration of the action) could be exerted without significant fatigue. However, the fact that performing the action using the maximum corrected force under the given conditions does not cause fatigue does not imply that it cannot be harmful to health. The tissues of the musculoskeletal system (joints, tendons and tendon sheaths, ligaments, muscles, etc.) have certain limits in their tolerance to stress that must be considered to establish the risk of the action.
To account for this tolerance to risk, a factor called risk multiplier (mr) is defined, whose value determines three possible risk zones. The risk based on the value of mr is obtained from the Table 5.
Assuming that for a given action it has been observed that the force applied by the user/worker is Fo, and that FBr is the Reduced Maximum Isometric Force calculated for that action, the following equation allows us to know the value of mr, and therefore the risk associated with the action by consulting the Table 5.
mr = Fo / FBr
On the other hand, if you want to establish the Maximum Recommended Force (FR) for a specific action for which we have calculated FBr, the same formula can be used but in the following form:
FR = mr * FBr
In this formula, giving mr the value of 0.5 would result in the Maximum Recommended Force (FR). Giving mr values between 0.5 and 0.7 would result in not recommended force intensities, and finally, assigning mr the value 0.7 would result in the lower limit of force intensities to avoid.
Risk Level mr Recommended ≤ 0.5 Not recommended > 0.5 - 0.7 To avoid > 0.7 Table 5:
Risk multiplier (mr)
The EN1005-3 standard establishes the three risk levels shown in Table 5. Each level implies making decisions about the necessary interventions to reduce the detected risk. According to the EN1005-3 standard, these would be:
| Risk Level | Required Intervention |
|---|---|
| Recommended | The risk of disorders or injuries is negligible. No intervention is necessary. |
| Not recommended | The risk of disorders or injuries cannot be ignored. Therefore, the risk should be assessed and analyzed more rigorously, considering additional risk factors, including those mentioned later in this document. This analysis may result in a risk multiplier value of 0.7 being considered acceptable. On the other hand, if the analysis concludes that the intended use of the machine involves a risk, a design modification or other measures aimed at reducing the risk may be necessary. |
| To avoid | The risk of disorders or injuries is evident and cannot be accepted. For this reason, measures must be taken to avoid it. |
Table 6:
Required intervention based on detected risk
The EN1005-3 standard makes certain initial assumptions regarding the efforts made. It is considered that the evaluated efforts are carried out in an optimal way and under ideal circumstances, that is, with the appropriate position of the limbs and trunk, within the permissible range of movement, with proper force application direction, and allowing for variation in the movements and efforts made. If the evaluated forces are not carried out under these conditions, as well as other conditions related to the work environment, psychosocial aspects, or personal protective equipment, the risk may be underestimated. The Table 7 lists the factors that, according to the EN1005-5 standard, should be considered as they can lead to an underestimation of the evaluated risk.
| Risk Factor | Description |
|---|---|
| Working posture | During the activity, the worker/user should be allowed to change their posture easily and frequently without movement restrictions. Moreover, they should avoid adopting postures in which their joints are in extreme positions. |
| Acceleration and movement precision | Efforts made with high acceleration cause increased stress on the tissues of the musculoskeletal system. Similarly, efforts made with movements that require precision lead to higher requirements. |
| Vibration | Vibrations are a risk factor for musculoskeletal disorders. Furthermore, the combination of efforts and vibrations can increase the independent risks of both. Machines should be designed to avoid transmitting vibrations to the worker. |
| Human-machine interaction | The worker must be able to control the pace of their work, being able to activate or deactivate the machines they control. |
| Personal protective equipment | Personal protective equipment may hinder the worker's movements. This should be taken into account during the design or evaluation of the workspace, considering the hindrance of movements or the decrease in strength they may cause. |
| Working environment | It is necessary to consider working space conditions such as lighting, noise, or thermal environment. Excessive temperature can quickly cause fatigue, while low temperatures may necessitate the use of coats or gloves, reducing mobility or dexterity. |
Table 7:
Additional risk factors
During Step A of the calculation process established by the method, it is necessary to calculate the Maximum Isometric Force (FB). Its calculation is not immediate and requires some knowledge of basic mathematics and statistics. The standard provides three possible alternatives of different accuracy and complexity for its calculation. Each of them can be used when certain conditions are met and assume certain simplifications in the calculation, except for Alternative 3, which performs an exact calculation. The software Forces - EN1005-3 provided by Ergonautas uses Alternative 3.
Alternative 1 is the simplest calculation procedure for the Maximum Isometric Force (FB). It uses the precalculated values of FB shown in Table 8. The values displayed in that table have been calculated using Alternative 3, considering the sex and age proportion of the European working population (shown in Table 1).
This calculation alternative should only be used when it is estimated that the user worker population is very large and follows the same sex and age distribution as the European working population. As a trade-off for its simplicity, it does not allow for the evaluation of actions performed by a specific user worker or by a group of user workers whose sex and age distribution is different from that of the European working population.
| Type of Action | Scope | |||
|---|---|---|---|---|
| Group | Action | Professional | Domestic | |
| Hand work | Grasping with the whole hand |  |
250 N | 184 N |
| Arm work in seated position | Upward |  |
50 N | 31 N |
| Downward |  |
75 N | 44 N | |
| Outward |  |
55 N | 31 N | |
| Inward |  |
75 N | 49 N | |
| Pushing with trunk support |  |
275 N | 186 N | |
| Pushing without trunk support |  |
62 N | 30 N | |
| Pulling with trunk support |  |
225 N | 169 N | |
| Pulling without trunk support |  |
55 N | 28 N | |
| Full-body work while standing | Pushing |  |
200 N | 119 N |
| Pulling |  |
145 N | 96 N | |
| Seated footwork with trunk support | Ankle action |  |
250 N | 154 N |
| Leg action |  |
475 N | 308 N | |
Alternative 2 is a simplified calculation procedure that allows estimating the Maximum Isometric Force (FB). Like the Calculation Alternative 1, it should only be used when the user worker population is estimated to be very large and follows the same sex and age distribution as the European working population, or when specific demographic data are not available. Like Alternative 1, it does not allow evaluating actions performed by a specific user worker or performed by a group of workers/users whose sex and age distribution is known and different from that of the European working population.
In this calculation alternative, the mean (F) and standard deviation (σ) values shown in the Table 9 are used to estimate the distribution of the Isometric Force, considering it as a normal distribution. The values in the table correspond to the adult female population, which is used as the reference group. Thus, this calculation procedure assumes simplifications regarding the distribution of forces and the reference group (adult women).
| Type of Action | Mean and standard deviation of Isometric Force distribution |
|||
|---|---|---|---|---|
| Group | Action | F | σ | |
| Hand work | Grip with whole hand |  |
278.0 N | 62.2 N |
| Arm work in seated position | Upwards |  |
58.0 N | 18.4 N |
| Downwards |  |
88.6 N | 33.2 N | |
| Outwards |  |
65.5 N | 26.2 N | |
| Inwards |  |
85.6 N | 24.6 N | |
| Pushing with trunk support |  |
312.0 N | 84.8 N | |
| Pushing without trunk support |  |
78.0 N | 42.7 N | |
| Pulling with trunk support |  |
246.0 N | 45.7 N | |
| Pulling without trunk support |  |
67.9 N | 33.5 N | |
| Full-body work standing |
Pushing |  |
233.7 N | 81.0 N |
| Pulling |  |
164.6 N | 44.9 N | |
| Seated footwork with trunk support |
Ankle action |  |
293.4 N | 104.7 N |
| Leg action |  |
542.5 N | 156.2 N | |
Based on the type of action being assessed, find the average value (F) and standard deviation (σ) in Table 9. These parameters define the Maximum Isometric Force distribution for the entire population as a normal distribution with an average value (F) and standard deviation (σ). The Figure 3 shows the distribution function of the Maximum Isometric Force for the action Full-body work pushing.
The standard establishes a population protection percentage of 85% when the calculation is performed for professional workers or users, and 99% when studying the general population or in a domestic context. Thus, knowing the distribution of the Maximum Isometric Force for the desired action, it is necessary to calculate the 15th percentile for professional workers or users, or the 1st percentile for the general population or domestic context.
Since we are dealing with low percentiles and working at one end of the distribution, the standard recommends performing a logarithmic transformation to calculate the percentile. This transformation is performed as follows:
Fln = ln F ; σln = ln [ (F + σ) / F ]
In the example of the action Full-body work pushing, shown in Figure 3, the value of Fln and σln for professional users or workers (15th percentile) would be:
After the transformation, the percentiles will be calculated as:
Fln% = Fln + Z% * σln
where:
Z% = Z15% = -0.5244 for professional workers or users.
Z% = Z1% = -2.0537 when studying the general population or in a domestic context.
Therefore, in the example of the action Full-body work pushing, shown in Figure 3, the value of Fln 15% for professional users or workers (15th percentile) will be calculated as:
Finally, it is necessary to undo the previous logarithmic scale transformation to return to the linear scale and obtain the Maximum Isometric Force (FB). This change is carried out as follows:
FB = exp (Fln)
In the example followed so far, the Maximum Isometric Force (FB) for the action Full-body work pushing for professional users or workers (15th percentile) will be:
Alternatives 1 and 2 for calculation are simplified calculation procedures that allow an estimation of the Maximum Isometric Force (FB). Each of them can be used when certain conditions are met and assume certain simplifications in the calculation. Alternative 3 performs a more accurate calculation and allows the assessment of specific users and workers or groups of workers with known specific sex and age distributions. The calculation process can be costly and requires some knowledge of mathematics and statistics. Therefore, it is advisable to use calculation software such as Forces - EN1005-3 provided by Ergoniza, which uses this calculation alternative.
Alternative 3 uses the mean (F) and standard deviation (σ) values shown in Table 10 to estimate the distribution of the Isometric Force considering it as a normal distribution. The values in the table correspond to women aged between 20 and 30 years, who are used as the reference group.
| Type of Action | Mean and standard deviation of Isometric Force distribution |
|||
|---|---|---|---|---|
| Group | Action | F | σ | |
| Hand work | Grip with whole hand |  |
270.0 N | 62.5 N |
| Arm work in seated position | Upwards |  |
56.0 N | 18.4 N |
| Downwards |  |
88.0 N | 33.2 N | |
| Outwards |  |
63.5 N | 26.2 N | |
| Inwards |  |
83.4 N | 24.6 N | |
| Pushing with trunk support |  |
303.0 N | 81.0 N | |
| Pushing without trunk support |  |
75.5 N | 42.7 N | |
| Pulling with trunk support |  |
242.0 N | 44.9 N | |
| Pulling without trunk support |  |
65.7 N | 33.5 N | |
| Full-body work standing |
Pushing |  |
228.0 N | 84.8 N |
| Pulling |  |
161.0 N | 45.7 N | |
| Seated footwork with trunk support |
Ankle action |  |
282,0 N | 96,5 N |
| Leg action |  |
528.5 N | 157.6 N | |
Based on the type of action being assessed, look for the mean (F) and standard deviation (σ) values in Table 10. With these parameters, the distribution of the Maximum Isometric Force for women aged between 20 and 30 years is defined as a normal distribution with a mean (F) and standard deviation (σ). Now, it is necessary to estimate the distributions for the remaining age and sex groups. The mean values and standard deviations of each group will be calculated as follows:
Women: Ffi = F * αfi ; σfi = σ * sfi
Men: Fmi = F * αmi ; σmi = σ * smi
| Means αxx | Standard deviations sxx | ||||||
|---|---|---|---|---|---|---|---|
| Age Groups | 1 | 2 | 3 | Age Groups | 1 | 2 | 3 |
| Women (αfi) | 0,96 | 1,00 | 0,93 | Women (sfi) | 1,03 | 1,00 | 0,96 |
| Men (αmi) | 1,95 | 2,16 | 1,70 | Men (smi) | 1,57 | 1,65 | 1,81 |
Table 11:
Multipliers for age and sex subgroups.
In these formulas, f and m refer to sex (female and male, respectively), and i indicates the age group, where 1 represents the group below 20 years, 2 represents the group between 20 and 50 years, and 3 represents the group above 50 years. The values of αfi and αmi are obtained from Table 11.
In this way, six distributions of Maximum Isometric Force will be obtained, one for each age and sex group, characterized by their means (Ff1, Ff2, Ff3, Fm1, Fm2, and Fm3) and their standard deviations (σf1, σf2, σf3, σm1, σm2 , and σm3). Figure 4 shows the distribution functions of the Maximum Isometric Force for the action Whole-body pushing. The red lines correspond to the female population of each Age Group, while the blue lines correspond to the male population. Calculating the 1st or 15th percentile of each distribution (depending on whether the population is professional or domestic) in the same way as indicated in Calculation Alternative 2 will yield the Maximum Isometric Force for each age and sex group. In Figure 4, these calculated values are shown for the action Whole-body pushing.
Since the goal is to calculate the Maximum Isometric Force for a specific population composition, it is necessary to weigh the distribution of each age and sex group by their relative size. In Figure 4, the weighted distribution (black line in the graph) has been calculated for the European working population. Finally, the resulting Maximum Isometric Force (FB) will be calculated in the same way as in Alternative 2, using the mean and standard deviation of the weighted distribution.
EN1005-3:2002+A1, 2009, Safety of machinery. Human physical performance. Part 3: Recommended force limits for machinery operation
Diego-Mas, J.A., 2015. Coplanar Static Biomechanical Analysis. Ergonautas, Polytechnic University of Valencia, 2015. Available online: https://www.ergonautas.upv.es/metodos/biomecanica/biomecanica-ayuda.php
Diego-Mas, Jose Antonio. Risk assessment for forces exerted in the workplace or when using machinery according to EN1005-3 standard. Ergonautas, Polytechnic University of Valencia, 2023.
A cloud based software that integrates more than 20 tools for managing the ergonomics of the workstations in your company.
Evaluate all ergonomic risk factors of the workstations in your company: inadequate postures, repetitive movements, load handling, thermal environment...

Use Artificial Intelligence for the automated detection of postures in photographs or videos.
Generate fully customizable reports in Microsoft Word or Adobe Pdf format.
In a multiuser environment so that your company can have access to your data everywhere.
You only need a free account on Ergoniza
ERGONIZA allows you to use Artificial Intelligence for postural load assessment. Automatically capture workers’ postures from a photograph or a video and obtain an automated evaluation of the risk associated with inadequate or forced postures.
AI in actionERGONIZA helps you manage the ergonomics of the workstations of your companies. Evaluate all the risk factors present in the workstations, manage the evaluations, and obtain editable and customizable reports.
You only need to register as a user of ERGONIZA to start testing.
Sign UpUnlock the full potential of Ergoniza. By becoming a Pro User you'll have access to all of Ergoniza and be able to use all of the online software without restrictions or time limits. You'll be able to use the results of evaluation methods and tools in your professional activity. You'll be able to print the results reports in pdf or Word and save your studies in files to open them later.
To register as a Pro user, you must first login to Ergoniza.
(*) In European Union countries, the price will be increased with the corresponding VAT.
(**) The price in american dollars has been calculated at the current exchange rate and may vary.
is a web by . Ergonautas is the specialized website in occupational ergonomics and ergonomic assessment of workstations at the . Ergonautas aims to be a useful support tool for the Occupational Risk Prevention and Ergonomics professional and people in training, providing rigorous technical information on occupational ergonomics, online tools for its application, research, training, and participation forums.
Ergonautas is formed by a large human team. In addition to technicians and programmers, the Ergonautas team is made up of researchers and professors from the Polytechnic University of Valencia. The team, led by José Antonio Diego Más, is at the forefront of research and teaching in ergonomics, teaching in official degrees and master's degrees, and developing research projects in the field of ergonomics and new technologies oriented towards humans.
If you need to know more, get in touch with Ergonautas
Or follow us on Linkedin
- - -
© 2006 - Universidad Politécnica de Valencia